数据处理与分析

Excel 2019 z-检验分析图解

z-检验工具对具有已知方差的平均值进行双样本z-检验。通过使用z-检验工具，可以检验两个总体平均值之间不存在差异的空值假设，而不是单方或双方的其他假设。而且，也可以使用z-检验确定两个汽车模型的性能差异。下面通过具体实例来详细讲解利用z-检验分析数据的操作技巧。

已知某公司两个部门的收入数据，使用“双样本平均差检验”分析工具对两个部门的收入数据进行分析，分析两个部门收入情况有无明显差异，具体操作步骤如下。

STEP01：打开“z-检验分析.xlsx”工作簿，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-105所示的“数据分析”对话框。在“分析工具”列表框中选择“z-检验：双样本平均差检验”选项，然后单击“确定”按钮。

图7-105　选择双样本平均差检验分析工具

STEP02：随后会打开“z-检验:双样本平均差检验”对话框，在“输入”列表区域设置变量1的区域为“$B$2:$B$13”，设置变量2的区域为“$C$2:$C$13”，设置变量1的方差为“5”，变量2的方差为“8”，并设置α的值为“0.05”，然后在“输出选项”列表中单击选中“新工作表组”单选按钮，最后单击“确定”按钮即可，如图7-106所示。

STEP03：此时，工作表中会显示“z-检验:双样本平均差检验”的分析结果，如图7-107所示。

图7-106　设置属性

图7-107　z-检验分析结果

Excel 2019 t-检验分析图解

t-检验工具用于判断每个样本，检验样本总体平均值是否相等。t-检验工具共分为3个工具，分别是平均值的成对二样本分析、双样本等方差假设和双样本异方差假设。

平均值的成对二样本分析

平均值的成对二样本分析可以确定取自处理前后的观察值是否具有相同总体平均值的分布。当样本中出现自然配对的观察值时，可以使用此工具成对检验。在“数据分析”对话框中，选择“t-检验:平均值的成对二样本分析”选项，然后单击“确定”按钮，打开“t-检验:平均值的成对二样本分析”对话框，如图7-99所示。

“平均值的成对二样本分析”对话框中的各项属性设置如下。

变量1的区域：需要统计的第1个样本。
变量2的区域：需要统计的第2个样本。
假设平均差：两个平均值之间的假设差异。
标志：指定数据的范围是否包含标签。
α(A)：表示检验的置信水平。
输出区域：存放统计结果的单元格区域，可以单击“输出区域”右侧的压缩按钮选择数据区域。
新工作表组：新建一个工作表，并将数据分析结果存放在新建工作表中。
新工作簿：新建一个工作簿，并将数据分析结果存放在新建工作簿中。

双样本等方差假设

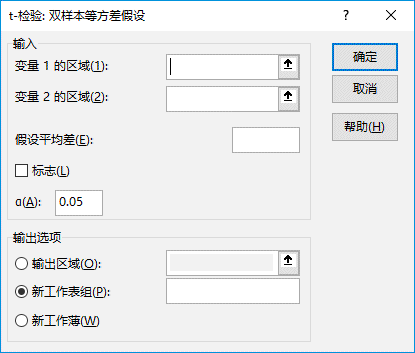
t-检验先假设两个数据集具有相同方差的分布，也称作同方差t-检验。可以使用t-检验来确定两个样本是否具有相同总体平均值的分布。在“数据分析”对话框中，选择“t-检验：双样本等方差假设”选项，然后单击“确定”按钮，打开“t-检验:双样本等方差假设”对话框，如图7-100所示。

图7-99　“t-检验：平均值的成对二样本分析”对话框

图7-100　“t-检验：双样本等方差假设”对话框

“t-检验：双样本等方差假设”对话框中的各项设置介绍如下。

变量1的区域：需要统计的第1个样本。
变量2的区域：需要统计的第2个样本。
假设平均差：两个平均值之间的假设差异。
标志：指定数据的范围是否包含标签。
α(A)：表示检验的置信水平。
输出区域：存放统计结果的单元格区域，可以单击“输出区域”右侧的压缩按钮选择数据区域。
新工作表组：新建一个工作表，并将数据分析结果存放在新建工作表中。
新工作簿：创建一个工作簿，并将数据分析结果存放在新建工作簿中。

双样本异方差假设

双样本异方差假设先假设两个数据集具有不同方差的分布，也称作异方差t-检验。与上面的“等方差”一样，可以使用t-检验来确定两个样本是否具有相同总体平均值的分布。当两个样本存在截然不同的对象时，可使用此检验。在“数据分析”对话框中，选择“t-检验：双样本异方差假设”选项，然后单击“确定”按钮，打开“t-检验：双样本异方差假设”对话框，如图7-101所示。

图7-101　“t-检验：双样本异方差假设”对话框

“双样本异方差假设”对话框中的各项设置介绍如下。

变量1的区域：需要统计的第1个样本。
变量2的区域：需要统计的第2个样本。
假设平均差：两个平均值之间的假设差异。
标志：指定数据的范围是否包含标签。
α(A)：表示检验的置信水平。
输出区域：存放统计结果的单元格区域，可以单击“输出区域”右侧的压缩按钮选择数据区域。
新工作表组：新建一个工作表，并将数据分析结果存放在新建工作表中。
新工作簿：新建一个工作簿，并将数据分析结果存放在新建工作簿中。

以上简单介绍了3种工具的使用方法，下面通过实例来具体讲解应用技巧。

打开“t-检验分析.xlsx”工作簿，已知两个零件的测试数值，使用“双样本等方差假设分析工具”对测试数据进行分析，具体操作步骤如下所示。

STEP01：切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-102所示的“数据分析”对话框。在“分析工具”列表框中选择“t-检验:双样本等方差假设”选项，然后单击“确定”按钮。

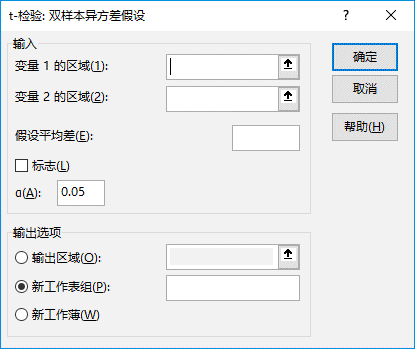
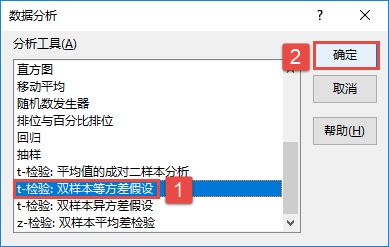
图7-102　选择双样本等方差假设分析工具

STEP02：随后会打开“t-检验:双样本等方差假设”对话框，在“输入”列表区域设置变量1的区域为“$B$2:$B$15”，设置变量2的区域为“$C$2:$C$15”，勾选“标志”复选框，并设置α的值为“0.05”，然后在“输出选项”列表中单击选中“新工作表组”单选按钮，最后单击“确定”按钮，如图7-103所示。

图7-103　设置属性

STEP03：此时，工作表中会显示“t-检验:双样本等方差假设”的分析结果，如图7-104所示。

图7-104　“t-检验：双样本等方差假设”分析结果

Excel 2019 F-检验分析图解

“F-检验双样本方差”分析工具，通过双样本F-检验对两个样本总体的方差进行比较。此分析工具可以进行双样本F-检验，又称为方差齐性检验，用来比较两个样本总体的方差是否相等。下面通过具体的实例来详细讲解利用“F-检验双样本方差”工具来分析数据的有关技巧。

图7-96　选择F-检验分析工具

STEP01：打开“F-检验分析.xlsx”工作簿，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-96所示的“数据分析”对话框。在“分析工具”列表框中选择“F-检验双样本方差”选项，然后单击“确定”按钮。

STEP02：随后会打开“F-检验双样本方差”对话框，在“输入”列表区域设置变量1的区域为“$B$2:$K$2”，设置变量2的区域为“$B$3:$K$3”，并设置α的值为“0.05”，然后在“输出选项”列表中单击选中“输出区域”单选按钮，设置输出区域为“$A$5”单元格，最后单击“确定”按钮，如图7-97所示。

图7-97　设置“F-检验　双样本方差”属性

STEP03：此时，工作表中会显示“F-检验双样本方差”的分析结果，如图7-98所示。

图7-98　计算分析结果

Excel 2019方差分析图解

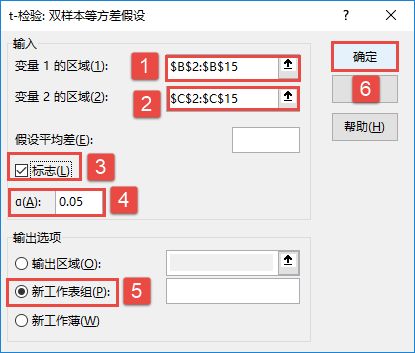
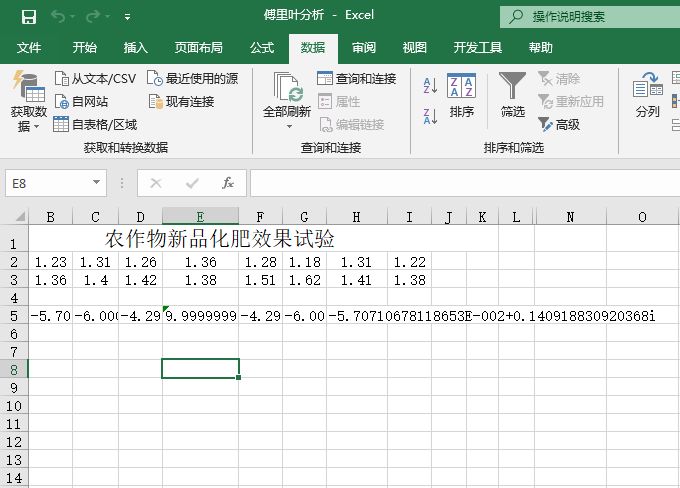
方差分析通常分为两种情况，一种是单因素方差分析，另一种是双因素方差分析。而双因素方差分析又可分为“无重复双因素方差分析”和“可重复双因素方差分析”两种。下面以“方差分析.xlsx”工作簿为例，逐一对这几种分析工具进行介绍。

单因素方差分析

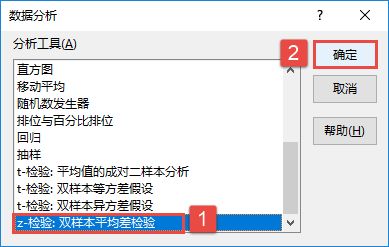
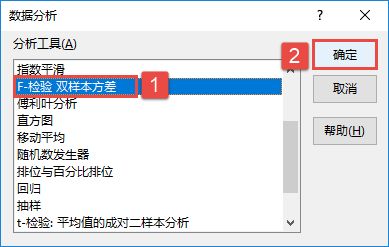
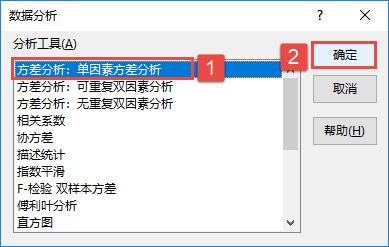
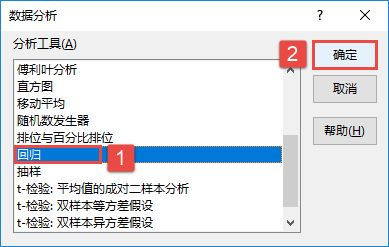
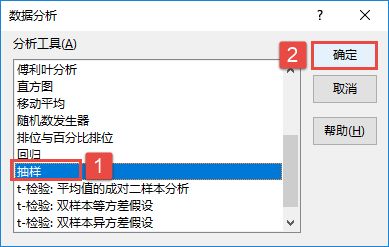
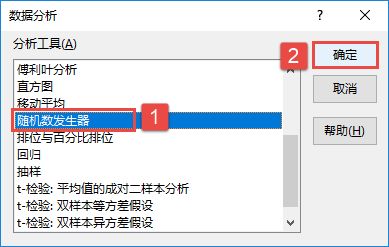
STEP01：打开“方差分析.xlsx”工作簿，切换至“单因素方差分析”工作表。在主页将功能区切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-85所示的“数据分析”对话框。在“分析工具”列表框中选择“方差分析：单因素方差分析”选项，然后单击“确定”按钮。

图7-85　选择单因素方差分析工具

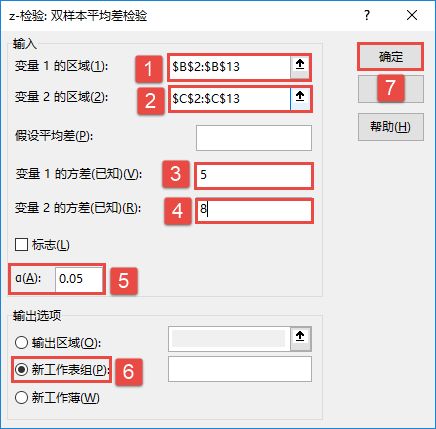
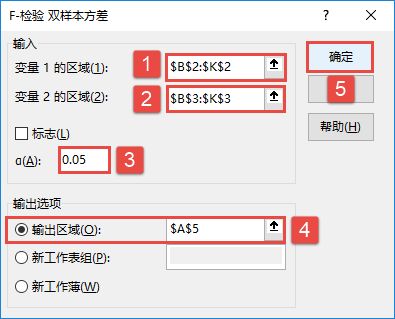
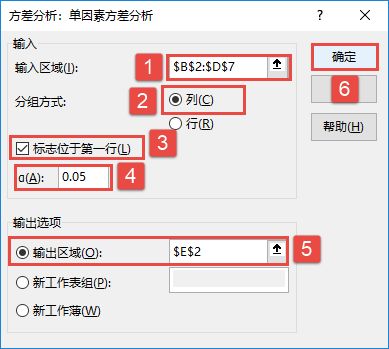
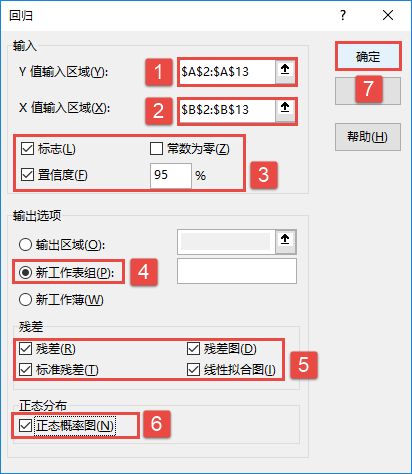
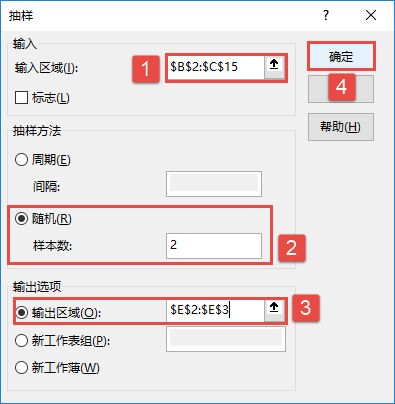
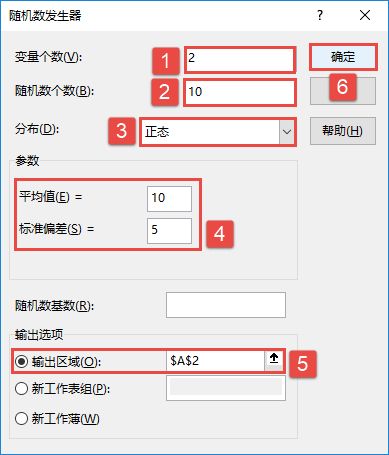
STEP02：随后会打开“方差分析：单因素方差分析”对话框，在“输入”列表区域设置输入区域为“$B$2:$D$7”，在“分组方式”列表中单击选中“列”单选按钮，并勾选“标志位于第一行”复选框，设置α的值为“0.05”。然后在“输出选项”列表中单击选中“输出区域”单选按钮，设置输出区域为“$E$2”单元格，最后单击“确定”按钮，如图7-86所示。

图7-86　“方差分析：单因素方差分析”对话框

对话框中各个设置项的作用简要介绍如下。

1）输入区域：在此输入待分析数据区域的单元格引用。该引用必须由两个或两个以上按列或行组织的相邻数据区域组成。例如这里选择单元格区域为“$B$2:$D$7”。

2）分组方式：指出输入区域中的数据是按行还是按列排列。例如这里选择分组方式为“列”。

3）标志位于第一行/列：如果输入区域的第1行中包含标志项，则可以选中“标志位于第一行”复选框；如果输入区域的第1列中包含标志项，则可以选中“标志位于第一列”复选框；如果输入区域没有标志项，则该复选框不会被选中，Excel将在输出表中生成数据标志。

4）α：根据需要指定显著性水平，例如这里输入“0.05”。

5）输出区域：如果用户选择“输出区域”单选按钮，则在右侧的文本框中输入或选择一个单元格地址。如果用户希望输出至新的工作表组中，则选择“新工作表组”单选按钮；如果用户希望输入至新的工作簿中，则选中“新工作簿”单选按钮。例如这里选择“输出区域”，在右侧的文本框中输入“$E$2”。

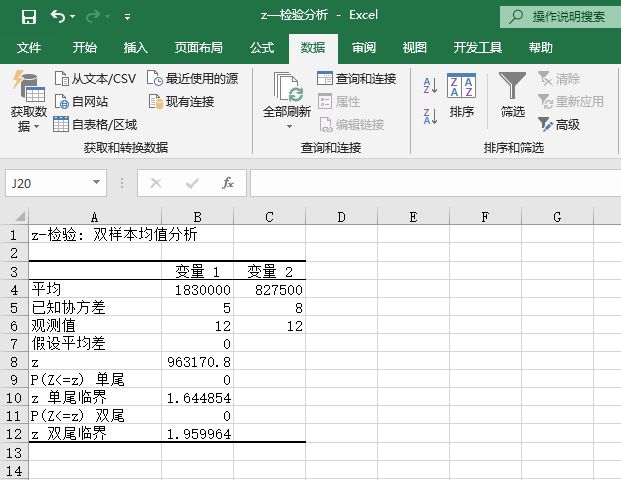
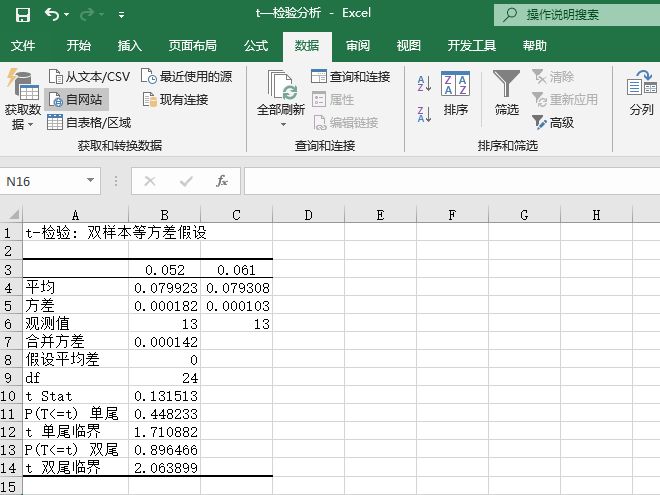
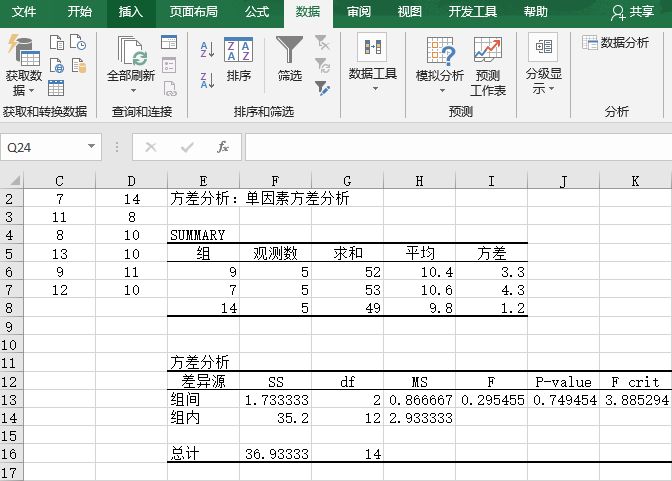
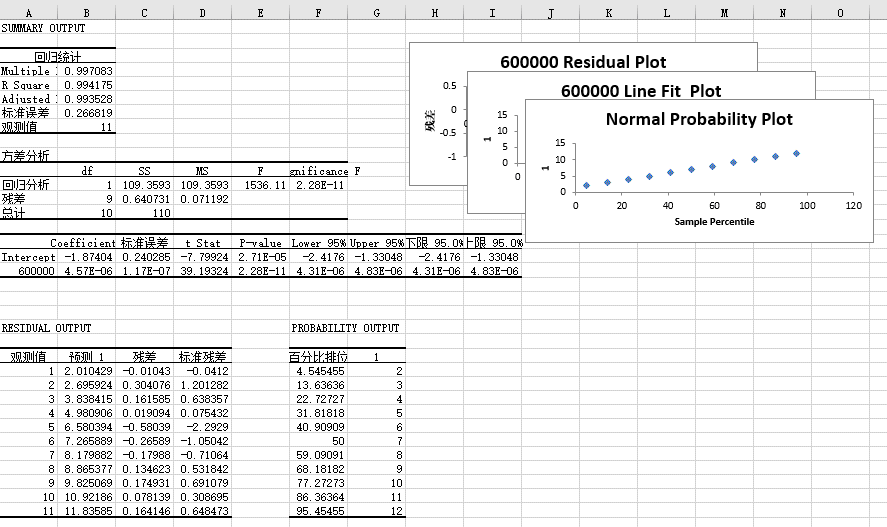
STEP03：此时，工作表中会显示“方差分析：单因素方差分析”的分析结果，如图7-87所示。

无重复双因素分析

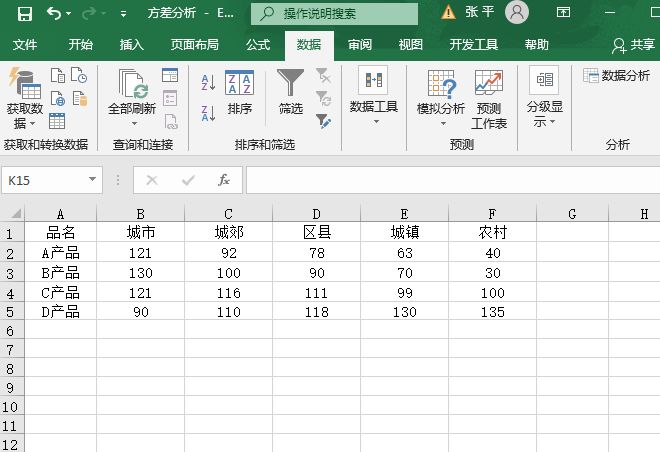
切换至“双因素方差分析–无重复性”工作表，如图7-88所示的数据表中说明的是某一种产品在5种不同的地点区域的销售情况。不在同区域、不同产品的情况下对销售的影响，即考察的区域不同、销售的产品不同对销售量是否有其显著影响。这两种因素组合只会产生一个销售数据，所以这是一个无重复双因素方差分析。因此，应该使用“无重复双因素分析”工具进行分析，其具体操作步骤如下。

图7-87　单因素方差分析结果

图7-88　“无重复性”数据表

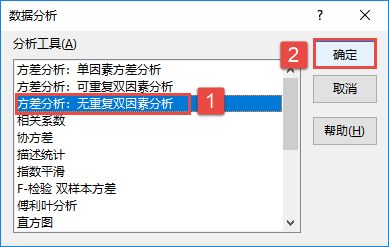
STEP01：切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-89所示的“数据分析”对话框。在“分析工具”列表框中选择“方差分析：无重复双因素分析”选项，然后单击“确定”按钮。

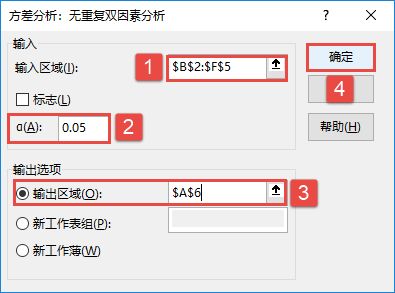
STEP02：随后会打开“方差分析：无重复双因素分析”对话框，在“输入”列表区域设置输入区域为“$B$2:$F$5”，设置α的值为“0.05”，然后在“输出选项”列表中单击选中“输出区域”单选按钮，设置输出区域为“$A$6”单元格，最后单击“确定”按钮，如图7-90所示。

图7-89　选择无重复双因素方差分析工具

图7-90　“无重复双因素分析”对话框

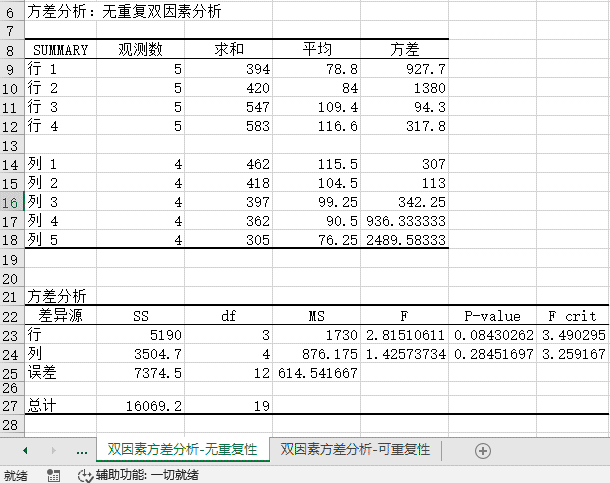
STEP03：此时，工作表中会显示“方差分析：无重复双因素分析”的分析结果，如图7-91所示。

可重复双因素分析

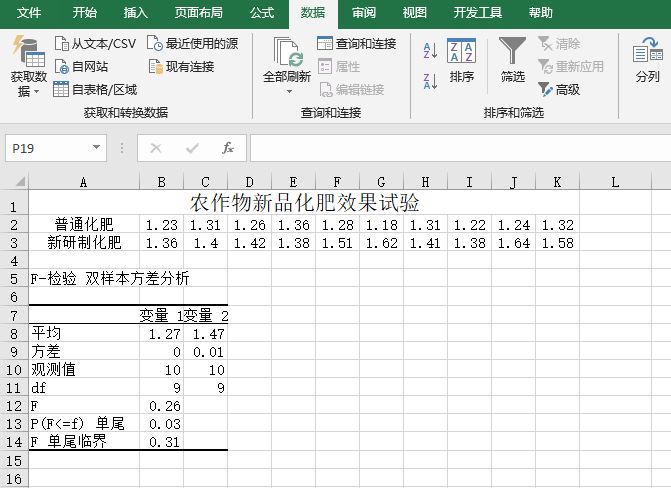
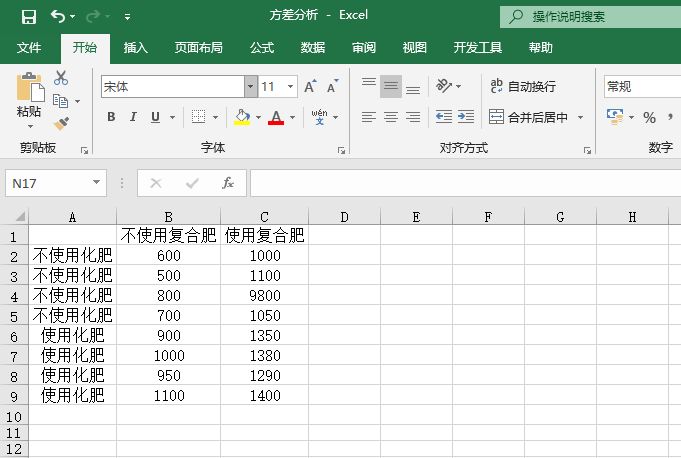
切换至“双因素方差分析–可重复性”工作表，如图7-92所示的工作表是一份农作物增收数据，其中化肥和复合肥是两个因素。目的是要考察化肥和复合肥的不同组合方案对农作物的收成是否有显著差异。从表中可以看到，每两个因素的组合都有4个数据，所以这是一个可重复性双因素方差分析，因此应该使用“可重复双因素分析”工具进行分析。

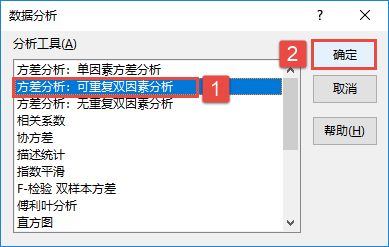
STEP01：切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-93所示的“数据分析”对话框。在“分析工具”列表框中选择“方差分析：可重复双因素分析”选项，然后单击“确定”按钮。

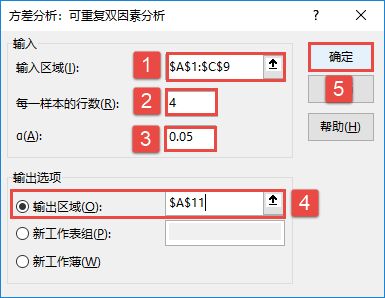
STEP02：随后会打开“方差分析：可重复双因素分析”对话框，在“输入”列表区域设置输入区域为“$A$1:$C$9”，在“每一样本的行数”文本框中输入“4”，并设置α的值为“0.05”，然后在“输出选项”列表中单击选中“输出区域”单选按钮，设置输出区域为“$A$11”单元格，最后单击“确定”按钮，如图7-94所示。

图7-91　无重复双因素方差分析结果

图7-92　农作物增收数据

图7-93　选择可重复双因素分析选项

图7-94　“可重复双因素分析”对话框

对话框中“每一样本的行数”项指的是每一样本的行数，因为在本实例中每一种方案都有4行数据，所以这里输入4。

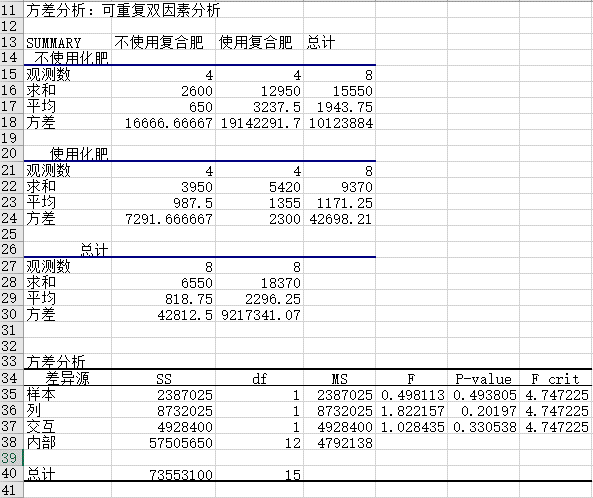
STEP03：此时，工作表中会显示“方差分析：可重复双因素分析”的分析结果，如图7-95所示。

图7-95　可重复双因素方差分析结果

Excel 2019回归分析图解

回归分析工具通过对一组观察值使用“最小二乘法”直线拟合来执行线性回归分析。本工具可以用来分析单个因变量是如何受一个或几个自变量的值影响的。下面通过具体的实例来详细讲解有关回归分析的操作技巧。

已知某公司2018年销售收入明细表，使用回归分析工具对收入、成本与费用进行分析。输入的原始数据如图7-81所示。

STEP01：切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-82所示的“数据分析”对话框。在“分析工具”列表框中选择“回归”选项，然后单击“确定”按钮。

图7-81　原始数据

图7-82　选择回归分析工具

STEP02：随后会打开“回归”对话框，在“输入”列表区域中设置Y值输入区域为“$A$2:$A$13”，设置X值输入区域为“$B$2:$B$13”，勾选“标志”复选框与“置信度”复选框，并设置置信度为“95%”。然后在“输出选项”列表区域中单击选中“新工作表组”单选按钮，在“残差”列表区域中依次勾选“残差”复选框、“残差图”复选框、“标准残差”复选框及“线性拟合图”复选框，最后在“正态分布”列表区域中勾选“正态概率图”复选框。设置完成后单击“确定”按钮即可返回工作表，如图7-83所示。

图7-83　设置属性

提示：在回归分析对话框中，各个属性值的含义如下。

1）Y值输入区域：独立变量的数据区域。

2）X值输入区域：一个或多个独立变量的数据区域。

3）标志：指定数据的范围是否包含标签。

4）常数为零：是否选择一个为零的常量。

5）置信度：表示置信水平。

6）输出区域：存放统计结果的单元格区域，可以单击“输出区域”右侧的压缩按钮选择数据区域。

7）新工作表组：新建一个工作表，并将数据分析结果存放在新建工作表中。

8）新工作簿：新建一个工作簿，并将数据分析结果存放在新建工作簿中。

9）残差：指定在统计结果中是否显示预测值与观察值的差值。

10）残差图：指定在统计结果中是否显示残差图的显示方式。

11）标准残差：指定在统计结果中是否显示标准残差的显示方式。

12）线性拟合图：指定在统计结果中是否显示线性拟合图的显示方式。

13）正态概率图：指定在统计结果中是否显示正态概率图的显示方式。

STEP03：此时，工作簿中会自动新建一个工作表，工作表中显示的回归分析效果如图7-84所示。

图7-84　回归分析的结果

Excel 2019抽样分析图解

抽样分析工具以数据源区域为总体的数据产生一个随机样本。当总体太大而不能进行处理或绘制时，可以选用具有代表性的样本。如果确认输入区域中的数据是周期性的，还可以对一个周期特定时间段中的数值进行采样。下面通过实例具体讲解该工具的使用技巧。

已知两个零件的测试数值，使用抽样分析工具对测试数值分析，并返回随机数。原始数据如图7-77所示。

图7-77　原始数据

STEP01：切换到“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-78所示的“数据分析”对话框。在“分析工具”列表框中选择“抽样”选项，然后单击“确定”按钮。

图7-78　选择抽样分析工具

STEP02：随后会打开“抽样”对话框，在“输入”列表区域中设置输入区域为“$B$2:$C$15”，在“抽样方法”列表区域中单击选中“随机”单选按钮，并设置样本数为“2”，然后在“输出选项”列表区域中单击选中“输出区域”单选按钮，设置输出区域为“$E$2:$E$3”，最后单击“确定”按钮完成设置，如图7-79所示。此时，工作表中显示的分析结果如图7-80所示。

图7-79　设置属性

图7-80　抽样分析结果

“抽样”对话框中的各项属性设置介绍如下。

1）输入区域：需要统计的数据区域。

2）标志：指定数据的范围是否包含标签。

3）周期：从输入区域内按固定间隔选择样品。

4）随机：选择样品的概率。

5）输出区域：存放统计结果的单元格区域，可以单击“输出区域”右侧的“压缩”按钮选择数据区域。

6）新工作表组：新建一个工作表，并将数据分析结果存放在新建工作表中。

7）新工作簿：新建一个工作簿，并将数据分析结果存放在新建工作簿中。

Excel 2019随机数发生器分析图解

“随机数发生器”分析工具可以使用几个分布之一产生一系列的按照要求的独立随机数，可以通过概率分布来表示总体中的主体特征。下面通过实例具体讲解使用“随机数发生器”工具来分析数据的操作技巧。

STEP01：新建一个工作簿，重命名为“随机数发生器分析”，切换至“Sheet1”工作表，可以先在工作表中输入需要产生随机数的变量列的变量名。此处假设有两个变量，输入字段名称后的工作表如图7-73所示。

STEP02：切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-74所示的“数据分析”对话框。在“分析工具”列表框中选择“随机数发生器”选项，然后单击“确定”按钮。

图7-73　输入字段名称

图7-74　选择“随机数发生器”分析工具

STEP03：随后会打开“随机数发生器”对话框，在“变量个数”文本框中输入“2”，在“随机数个数”文本框中输入“10”。单击“分布”选择框右侧的下拉按钮，在展开的下拉列表中选择“正态”选项，在“参数”列表区域中设置平均值为“10”，标准偏差为“5”。在“输出选项”列表区域中单击选中“输出区域”单选按钮，并设置输出区域为“$A$2”单元格，最后单击“确定”按钮，如图7-75所示。此时，可以看到如图7-76所示的分析结果。

图7-75　设置属性

图7-76　随机数发生器分析结果

在“随机数发生器”对话框中，“分布”右侧的下拉列表框中共包含多种创建随机数的分布方法，下面逐一进行介绍。

1）均匀：以下限和上限来表征。其变量值通过对区域中的所有数值进行等概率抽取而得到。普通的应用使用范围是0～1的均匀分布。

2）正态：以平均值和标准偏差来表征。普通的应用使用平均值为0、标准偏差为1的标准正态分布。

3）伯努利：以给定的试验中成功的概率（p值）来表征。伯努利随机变量的值为0或1。

4）二项式：以一系列试验中成功的概率（p值）来表征。

5）泊松：以值a来表征，a等于平均值的倒数。泊松分布经常用于表示单位时间内事件发生的次数。

6）模式：以下界和上界、步幅、数值的重复率和序列的重复率来表征。

7）离散：以数值及相应的概率区域来表征。该区域必须包含两列，左边一列包含数值，右边一列为与该行中的数值相对应的发生概率。所有概率的和必须为1。

Excel 2019移动平均分析图解

“移动平均”分析工具可以基于特定的过去某段时期中变量的平均值，对未来值进行预测。移动平均值提供了由所有历史数据的简单的平均值所代表的趋势信息。使用该工具可以预测销售量、库存或者其他趋势。下面通过具体实例来详细介绍该工具的操作技巧。

已知B产品在5月份的销量，利用“移动平均”分析工具，分析其销售趋势。具体操作步骤如下。

STEP01：打开“移动平均分析.xlsx”工作簿，切换到“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-70所示的“数据分析”对话框。在“分析工具”列表框中选择“移动平均”选项，然后单击“确定”按钮。

STEP02：随后会打开“移动平均”对话框，在“输入”列表区域设置输入区域为“$C$4:$C$34”，勾选“标志位于第一行”复选框，在“间隔”文本框中输入“7”，然后在“输出选项”列表区域中设置输出区域为“$D$3”单元格，并勾选“图表输出”复选框和“标准误差”复选框，最后单击“确定”按钮，如图7-71所示。此时，在工作表中可以看到如图7-72所示的分析结果。

图7-70　选择移动平均分析工具

图7-71　设置属性

在“移动平均”对话框中，有一个“标准误差”复选框选项，该选项指定在输出表的一列中包含标准误差值。如果选中该复选框，Excel将生成一个两列的输出表，其中左边一列为预测值，右边一列为标准误差值。如果没有足够的源数据来进行预测或者计算标准误差值，Excel会返回错误值“#N/A”。

图7-72　移动平均分析结果

Excel 2019傅利叶分析图解

“傅利叶分析”分析工具可以解决线性系统问题，而且可以通过快速傅利叶变换进行数据变换来分析周期性的数据。此外，该工具还支持逆变换，即通过对变换后的数据的逆变换返回初始数据。下面通过具体实例对该工具的使用技巧进行详细阐述。

STEP01：打开“傅利叶分析.xlsx”工作簿，切换到“数据”选项卡，然后在“分析”组中单击“数据分析”按钮打开如图7-67所示的“数据分析”对话框。在“分析工具”列表框中选择“傅利叶分析”选项，然后单击“确定”按钮。

图7-67　选择傅利叶分析工具

STEP02：随后会打开“傅利叶分析”对话框，在“输入”列表区域设置输入区域为“$B$2:$I$2”，然后在“输出选项”列表中单击选中“输出区域”单选按钮，并设置输出区域为“$A$5”单元格，最后单击“确定”按钮，如图7-68所示。此时，在工作表中可以看到如图7-69所示的分析结果。

图7-68　设置属性

图7-69　傅利叶分析的结果

Excel 2019直方图分析图解

“直方图”分析工具可计算数据单元格区域和数据接收区间的单个核累积频率。此工具可用于统计数据集中某个数值出现的次数。下面通过具体实例，来详细讲解利用“直方图”工具来分析数据的应用操作技巧。

STEP01：打开“直方图分析.xlsx”工作簿，切换到“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-64所示的“数据分析”对话框。在“分析工具”列表框中选择“直方图”选项，然后单击“确定”按钮。

STEP02：随后会打开“直方图”对话框，在“输入”列表区域设置输入区域为“$C$4:$C$16”，接收区域为“$E$4:$E$14”，然后在“输出选项”列表中单击选中“输出区域”单选按钮，并设置输出区域为“$A$18”单元格，依次勾选“柏拉图”复选框、“累积百分率”复选框和“图表输出”复选框，最后单击“确定”按钮，如图7-65所示。此时，在工作表中看到分析结果，该结果中还包含数据分析图表，如图7-66所示。

图7-64　选择直方图分析工具

图7-65　设置直方图属性

图7-66　直方图分析结果